|
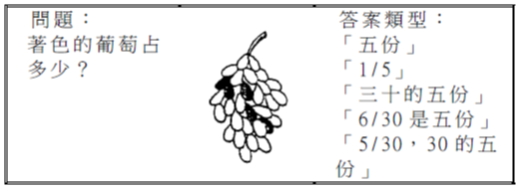
(二)為什麼學生學習分數基本概念時會產生迷思概念? 1. 忽略單位量 Figueras, Filloy& Volderuoros(1987,引自呂玉琴,1991)和Figueras(1989,引自呂玉琴,1991)指出學生在學習分數基本概念時,有時候會忽略給定的單位量。在下圖左邊,學生忽略左邊的橘子,只注意到右邊有被圈起來的橘子,而說是 。下圖中間,學生只圈出和分母數字相同的磚塊數來代表單位量,再圈出分子的數量,來代表 。下圖右邊,學生無法將整個圖形當做單位量,而將圖形二看成陰影部份和空白部份的比較結果。 學生為什麼會忽略單位量呢?我們分析題目,發現題目的單位量是被隱藏著,也就是沒有特別突顯單位量,因此學生心較容易產生迷思概念。假如,我們改成「圈起來的橘子佔全部的多少?」「將全部磚塊的 」「陰影部份占這個圖形的幾分之幾?」相信學生就比較不會產生迷思概念。 此外,我們也發現到,在教學時,老師或者學生時常忘了說出它的單位,也就是對於問題「一個蛋糕平分8份,其中的3份是多少?」學生時常回答「 」,而不是說「 個」或者「 個蛋糕」。久而久之就沒有特別注意單位量。又因為「一個蛋糕平分8份,其中的3份是多少?」這句比較長,同時在剛教分數時,都是用一個蛋糕,因此,有些學生就不說出一個蛋糕,僅僅說「8份中的3份是多少?」久而久之,對忘了單位量的重要性。有時候,它和學生的記憶力有關,有些學生無法記得太長的句子,僅記得「8份中的3份是多少?」 2. 受分子或者分母控制 有些學生在回答分數基本概念的問題時,只考慮到分子的部份,因此下圖問「著色的葡萄占多少?」時,只看到著色的部份只有5個,而回答「五份」,我們稱學生的分數基本概念受分子控制或者受分子影響。 有些學生在回答分數基本概念的問題時,只考慮到分母的部份,因此下圖左邊要學生「圈出四分之三朵花」時,只看圈出四朵花。下圖右邊請學將沒有畫出的氣球補上去,學生將只有一個氣球的孤立,不去理它;其他每串氣球都補上去,讓每串的氣球個數等於分母5。犯此類迷思的學生,我們說他的分數基本概念受分母控制或者受分母影響。 為什麼學生會分子控制呢?我們發現老師在教學時,有時候要學生說出「一個蛋糕平分8份,其中的3份是多少?」,因為太長,且有時候都是在平分成8塊下來解題,因此簡略的說成「3份是多少?」久而久之,就以為3份是 。有時候,它和學生的記憶力有關,有些學生無法記得太長的句子,僅記得「3份是多少?」
| 
 發表於 2014-7-4 20:00:04
發表於 2014-7-4 20:00:04